Numerical simulations of
the investigated experimental configurations were performed using finite-volume
commercial code Fluent 6.1.18 (Fluent Inc., USA). Spatial derivatives were
approximated using QUICK scheme, which is based on a weighted average of
second-order-upwind and central interpolation of the variable. Pressure-velocity
coupling was done using SIMPLE algorithm. Solutions were obtained by direct
simulations of the flow for two-dimensional and three-dimensional uniform
structural mesh using double precision solver. The solutions when residuals
approach given value 10-5 and 10-6, respectively.
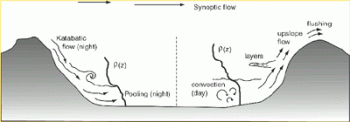
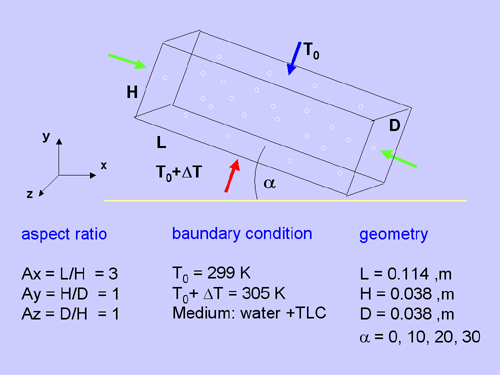
A numerical investigation has been made of two-dimensional natural convection of
water in an externally heated vertical or inclined rectangular cavity containing
uniformly distributed internal energy sources. Results have been obtained for
Rayleigh number up to 106 and inclined of 0, 10, 20, 30, 40,
50, 60, 70, 80, 90 deg.
The
Fluent package 6.0.20. have been used to solve unsteady Navier-Stokes equations for
dwo-dimensional in rectangular cavity. The
governing partial differential equations are the ones express the conservation
of mass momentum and energy using the Boussinesq approximation.